第1节 函数
一、基础题
1.求下列函数值:
(1) 设$f(x)=\arcsin x$,求$f(0),f(-1),f\left(\frac{\sqrt3}{2}\right),f\left(-\frac{\sqrt2}{2}\right)$ 解答:
$$f(0)=\arcsin 0=0$$$$f(-1)=\arcsin(-1)=-\frac{\pi}{2}$$$$f\left(\frac{\sqrt3}{2}\right)=\arcsin\left(\frac{\sqrt3}{2}\right)=\frac{\pi}{3}$$$$f\left(-\frac{\sqrt2}{2}\right)=\arcsin\left(-\frac{\sqrt2}{2}\right)=-\frac{\pi}{4}$$.
(2) 设
$$f(x)= \begin{cases} |\cos x|,\ |x|<\frac{\pi}{3},\\[6pt] 0,\ |x|\ge \frac{\pi}{3}, \end{cases}$$求$f\left(\frac{\pi}{4}\right),f\left(-\frac{\pi}{6}\right),f(-3)$。 解答:
$$\left|\frac{\pi}{4}\right|<\frac{\pi}{3},\quad f\left(\frac{\pi}{4}\right)=|\cos \frac{\pi}{4}|=\frac{\sqrt2}{2}$$$$\left|-\frac{\pi}{6}\right|<\frac{\pi}{3},\quad f\left(-\frac{\pi}{6}\right)=|\cos(-\frac{\pi}{6})|=\frac{\sqrt3}{2}$$$$|-3|> \frac{\pi}{3},\quad f(-3)=0$$.
2.下列函数中,哪些是偶函数?哪些是奇函数?哪些既非奇又非偶函数?
(1) $y=x^2(1-x^2)$
解答:
$$f(-x)=(-x)^2(1-(-x)^2)=x^2(1-x^2)=f(x)$$为偶函数。
(2) $y=\ln\frac{x-1}{x+1}$
解答:
$$f(-x)=\ln\frac{-x-1}{-x+1}=\ln\frac{-(x+1)}{-(x-1)}=\ln\frac{x+1}{x-1}=-f(x)$$为奇函数。
(3) $y=\frac{1-x^2}{\cos x}$
解答: 分子是偶函数,分母是偶函数,因此整体为偶函数。
(4) $y=\frac{a^x+a^{-x}}{2}$
解答:
$$f(-x)=\frac{a^{-x}+a^{x}}{2}=f(x)$$为偶函数。
(5) $y=\arcsin x-\cos x+1$
解答: $\arcsin x$是奇函数,$-\cos x$是偶函数,加常数1破坏对称,因此非奇非偶。
(6)
$$y= \begin{cases} -x^2+x,\ x>0,\\[4pt] x^2-x,\ x<0. \end{cases}$$解答: 要验证奇偶性,需要分别计算 $f(-x)$ 与 $\pm f(x)$。 令 $x>0$(只需考虑正的,再用定义): 原函数在 $x>0$ 时:
$$f(x)=-x^2+x.$$计算 $f(-x)$: 因为 $-x<0$,应代入第二段:
$$f(-x)=(-x)^2-(-x)=x^2+x.$$现在比较:
$$f(-x)=x^2+x,\qquad -f(x)= -(-x^2+x)=x^2-x.$$显然:
$$f(-x)\ne f(x),\qquad f(-x)\ne -f(x).$$因此该函数 既不是奇函数,也不是偶函数。
3.设$f(x)$为定义在$(-a,a)$内的偶函数,且$f(x)$在$(0,a)$内单调递减,证明:$f(x)$在$(-a,0)$内单调递增$(a>0)$。
解答:
任取$-a 则 且
于是
$$f(x_2)=f(-x_2)>f(-x_1)=f(x_1).$$即 $f(x)$ 在 $(-a,0)$ 上单调递增。
4.求下列函数的反函数:
(1) $y=\sqrt[3]{x-1}$
解答:
$$y=\sqrt[3]{x-1}\ \Rightarrow\ x-1=y^3\ \Rightarrow\ x=y^3+1$$反函数:
$$f^{-1}(x)=x^3+1.$$.
(2) $y=\frac{1-2x}{1+2x}$
解答:
$$y(1+2x)=1-2x$$$$y+2xy=1-2x$$$$2x(y+1)=1-y$$$$x=\frac{1-y}{2(y+1)}$$反函数:
$$f^{-1}(x)=\frac{1-x}{2(x+1)}.$$.
(3) $y=2\sin 3x\quad \left(\frac{\pi}{6}\le x\le\frac{\pi}{6}\right)$
解答:
$$\sin 3x=\frac{y}{2}$$$$3x=\arcsin\frac{y}{2}$$$$x=\frac{1}{3}\arcsin\frac{y}{2}$$反函数:
$$f^{-1}(x)=\frac{1}{3}\arcsin\frac{x}{2}.$$.
(4) $y=\frac{3^x}{1+3^x}$ 解答:
$$y(1+3^x)=3^x$$$$y+y_{3}^x=3^x$$$$y=3^x(1-y)$$$$3^x=\frac{y}{1-y}$$$$x=\log_3\frac{y}{1-y}$$反函数:
$$f^{-1}(x)=\log_3\frac{x}{1-x}.$$.
二、提高题
5.设
$$f(x)= \begin{cases} (x-1)^2,\ x\le 1,\\[4pt] \frac{1}{1-x},\ x>1, \end{cases} \quad g(x)= \begin{cases} 2x,\ x>0,\\ 3x,\ x\le 0. \end{cases}$$求$f[g(x)]$。 解答: 考虑$g(x)$的取值范围:
若$x>0$,则$g(x)=2x>0$,需区分$2x\le1$ 与 $2x>1$。
$$2x\le1\ \Rightarrow\ x\le\frac12,\quad f(g(x))=(2x-1)^2.$$$$2x>1\ \Rightarrow\ x>\frac12,\quad f(g(x))=\frac{1}{1-2x}.$$若$x\le0$,则$g(x)=3x\le0\le1$,取第一段:
$$f(g(x))=(3x-1)^2.$$最终:
$$f[g(x)]= \begin{cases} (3x-1)^2,\ x\le0,\\[4pt] (2x-1)^2,\ 06.设
$$f(x)= \begin{cases} 1,\ |x|\lt 1,\\ 0,\ |x|=1,\\ -1,\ |x|\gt 1,\\ \end{cases} \quad g(x)=e^x.$$求$f[g(x)]$和$g[f(x)]$,并画出两个函数的图形。
解答: 一、求 $f[g(x)]$ 先判断 $g(x)=e^x$ 的取值范围:
$$e^x>0,\quad \forall x.$$因此只需讨论 $e^x$ 与 1 的大小关系。
情况 1:$|g(x)|<1$ 即:
$$e^x<1 \quad \Longleftrightarrow\quad x<0.$$此时:
$$f[g(x)]=1.$$情况 2:$|g(x)|=1$ 即:
$$e^x=1 \quad \Longleftrightarrow\quad x=0.$$因此:
$$f[g(0)]=0.$$情况 3:$|g(x)|>1$ 即:
$$e^x>1 \quad \Longleftrightarrow\quad x>0.$$因此:
$$f[g(x)]=-1.$$
结果
$$f[g(x)]= \begin{cases} 1,\ x<0,\\[4pt] 0,\ x=0,\\[4pt] -1,\ x>0. \end{cases}$$二、求 $g[f(x)]$ 利用:
$$f(x)= \begin{cases} 1,\ |x|<1,\\ 0,\ |x|=1,\\ -1,\ |x|>1, \end{cases}$$代入 $g(x)=e^x$ 得:
若 $|x|<1$
$$f(x)=1 \quad\Rightarrow\quad g[f(x)]=e^1=e.$$若 $|x|=1$
$$f(x)=0 \quad\Rightarrow\quad g[f(x)]=e^0=1.$$若 $|x|>1$
$$f(x)=-1 \quad\Rightarrow\quad g[f(x)]=e^{-1}=\frac{1}{e}.$$
结果
$$g[f(x)]= \begin{cases} e,\ |x|<1,\\[4pt] 1,\ |x|=1,\\[4pt] \dfrac1e,\ |x|>1. \end{cases}$$三、图形
- $f[g(x)]$ 的图形
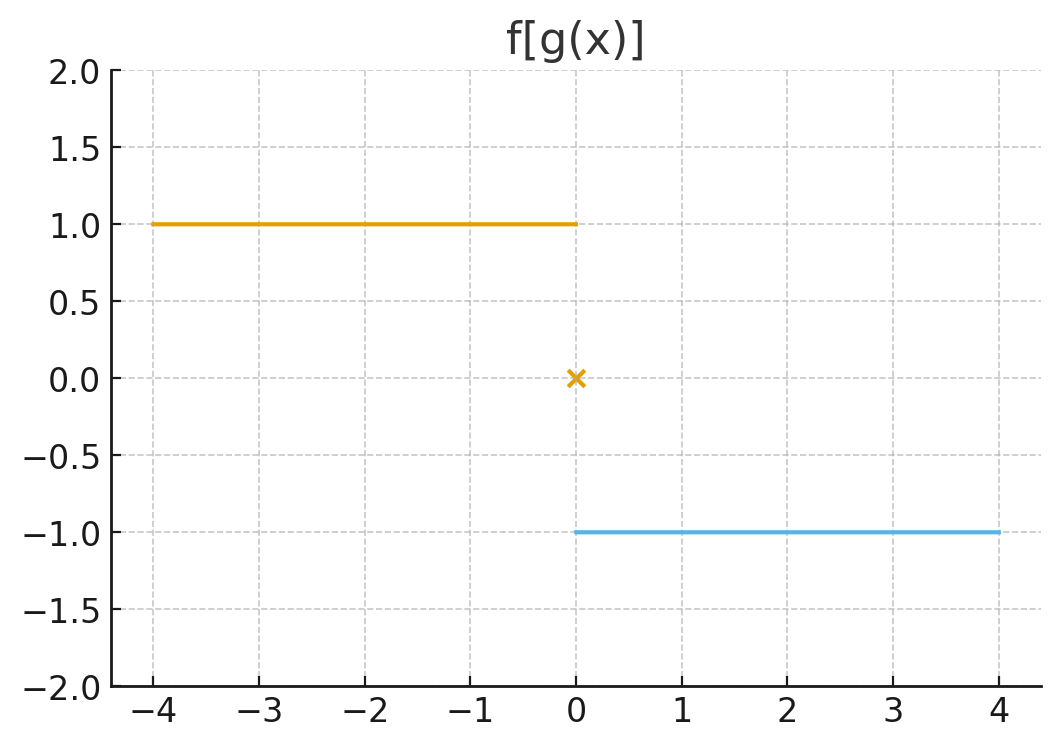
这是一个三段常值函数:
当 $x<0$ 时,函数值为 1(水平线段)
当 $x=0$ 时,函数值为 0(单独的点)
当 $x>0$ 时,函数值为 -1(水平线段)
图形形状:三段水平直线,中间“跳变”,在 $x=0$ 处为 0 点。
- $g[f(x)]$ 的图形
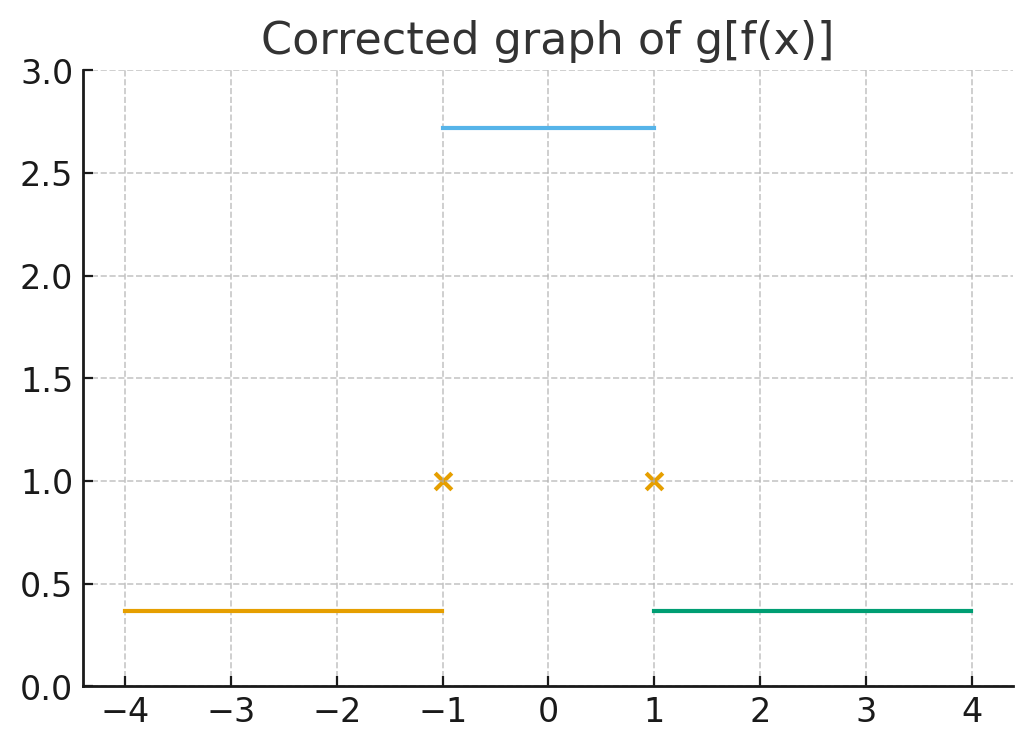
分三段水平线:
区间 $(-1,1)$ 上恒为 $e$
点 $x=\pm 1$ 时取值为 1
区间 $(-\infty,-1)\cup(1,\infty)$ 上恒为 $1/e$
图形为三段水平线,中间高,两边低,在 $x=\pm1$ 处为单独的点。
三、考研真题
7.(19900306)设函数$f(x)=xe^{\sin x}\tan x$,则$f(x)$是( )。
A. 偶函数 B. 无界函数 C. 周期函数 D. 单调函数
解答:
分别判断:
$$f(-x)=(-x)e^{\sin(-x)}\tan(-x)=(-x)e^{-\sin x}(-\tan x)=xe^{-\sin x}\tan x\neq\pm f(x),$$故不是奇偶函数,排除A。 当$x\to \frac{\pi}{2}^-$,$\tan x\to +\infty$,且$xe^{\sin x}>0$,故
$$f(x)\to +\infty,$$为无界函数,应选B。 该函数包含$x$,不是周期函数,排除C。 同时在不同区间符号改变与震荡,不可能是单调函数,排除D。 正确答案:B